What is a Qubit?
Bits and development of modern computers
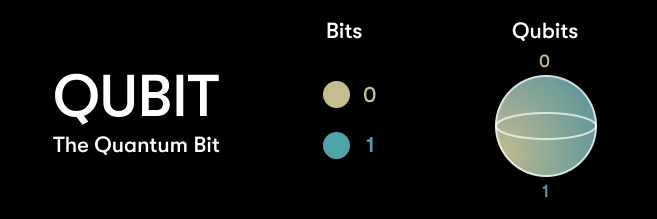
In classical computer science, the fundamental unit of information is the bit, which is a binary system. A bit can be in one of two states: 0 or 1. This simple binary system forms the foundation of traditional computing.
The physical realization of bits has significantly evolved over time, with transistors playing a crucial role in this development. Transistors are electronic semiconductor components, which control the flow of electricity in devices, and can switch between two states - high and low voltage - making them an ideal physical candidate to realize huge numbers of bits in modern computing systems.
The invention of the transistor in the mid-20th century revolutionized the field and resulted in the development of smaller, faster, and more efficient computers
[1]. This invention marked a significant milestone in the history of computing, and the engineers John Bardeen, Walter Brattain, and William Shockley from Bell Laboratories received the Nobel Prize in Physics for their invention in 1956.
Qubits and information in the quantum world
In quantum computing, the fundamental unit of information is a qubit, which is physically encoded in a two-level quantum system. These two levels are known as the ‘computational basis states’, and we usually write them as ∣0⟩ and ∣1⟩. These correspond directly to the 0 and 1 states of a classical bit.
However, unlike a classical bit that can only be in one state at a time (either 0 or 1), a qubit can be in a state that is in a linear superposition of basis states. This is unique to quantum computing and doesn’t have an equivalent in classical computing. A general qubit state can therefore be described as |ψ⟩= α1∣0⟩ + α2∣1⟩, which is a linear superposition of ∣0⟩ and ∣1⟩ with complex amplitudes α1 and α2.
The state of a qubit in a superposition remains in this state as long as the qubit is not measured or disturbed. However, as soon as a measurement is made, the qubit settles into one of its basis states, either ∣0⟩ or ∣1⟩, and the superposition is destroyed. This process is known as ‘collapse’, and it’s a fundamental feature of measurement in quantum mechanics. If we measure the qubit, we obtain the ∣0⟩ state with probability |α1|2 and the ∣1⟩ state with probability |α2|2 , where the sum of both needs always equal to one (|α1|2 + |α2|2 = 1) [2].

Types of Qubits
Currently, there are a few qubit implementations that look quite promising for the realization of a quantum computer. The most prominent examples are superconducting qubits, ion traps and spin qubits and photons.
1. Spin: Spin-based qubits use the spin of charge carriers, such as electrons, confined in a semiconductor material as the basis for information storage. The spin degree of freedom of that electron provides a natural two-level system that is insensitive to electric fields, leading to relatively long quantum coherence times. The first spin qubit quantum computer was proposed by Daniel Loss and David P. DiVincenzo in 1997 [3]. Intel has raised efforts to develop quantum computers based on silicon spin qubits in recent years [4].
2. Trapped Atoms and Ions: In trapped-ion quantum computing, ions are confined and suspended in free space using electromagnetic fields. Qubits are defined by two distinct energy states of the ions, and quantum information can be transferred through the collective quantized motion of the ions in a shared trap. The fundamental operations of a quantum computer have been demonstrated experimentally with high accuracy in trapped-ion systems [5,6].
Neutral atoms, on the contrary, are trapped by highly focused laser beams, so-called optical-tweezers. Qubits are encoded in distinct electronic energy states of the atoms, and their quantum state may be manipulated via laser pulses. As for breakthroughs, researchers at ETH Zurich have managed to trap ions using static electric and magnetic fields and perform quantum operations on them. This new ion trap could be used to realize quantum computers with far more quantum bits than have been possible up to now [7]. On the neutral atoms side, a team of researchers at Harvard created the first programmable, logical quantum processor, capable of encoding up to 48 logical qubits and executing hundreds of logical gate operations [8].
3. Photons: Photons, the quantum particles of light, can serve as qubits, too. They are natural candidates for quantum communication due to their favorable properties in speed, coherence, and low propagation loss. This makes them ideal for transmitting quantum information over long distances. Moreover, photons offer various degrees of freedom where quantum information can be encoded. For example, two distinct propagation paths, or the polarisation degree of freedom, which is the orientation of the photon’s electric field, may serve as a two-level system to encode and manipulate a qubit [9].
4. Superconducting Circuits: Superconducting circuits are among the leading physical implementations of qubits. They are tiny circuits made out of superconducting materials that can carry an electric current without resistance when cooled to very low temperatures. These circuits can behave like artificial atoms, absorbing and emitting energy at specific frequencies, which makes them suitable for use as qubits [10].
In a superconducting circuit, the quantum state of the circuit (the qubits) can be controlled using microwave pulses. These pulses can manipulate the qubit into a superposition of states, flip its state, or entangle it with other qubits. This is how quantum operations, or gates, are performed in a superconducting quantum computer. Companies like IBM, Google, and Rigetti are using superconducting circuits to build their quantum computers. These companies have already built quantum processors with hundreds to thousands of qubits and are working on scaling up their technology to create larger, more powerful quantum computers [11].
Visualization of Qubits
Qubit states can be visualized in different ways. Below are the most common ones.
- 1. Bloch Sphere: The Bloch Sphere is a mathematical tool used to represent all possible states of a single qubit. It’s a 3D representation where each qubit state is represented as a point on the surface of the sphere. The north and south poles typically represent the two computational states [12].
- 2. Q-Sphere: The Q-Sphere is a visualization tool used in quantum computing to represent the state of multiple qubits. Unlike the Bloch Sphere, which represents the state of a single qubit, the Q-Sphere can represent transformations between different multi-qubit states. Here, the size of the points is proportional to the probability of the corresponding term in the state and the color represents the relative phase between the basis states.
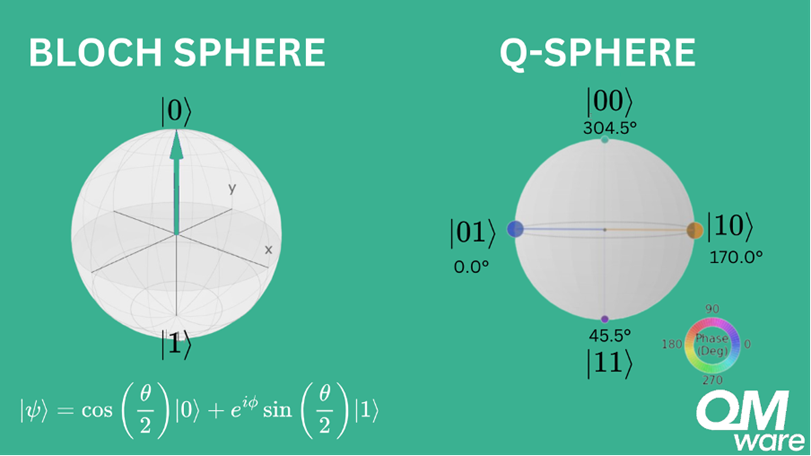
To try these visualizations, qiskit offers great tools for visualizing qubits. You can use the plot_bloch_vector function for Bloch Sphere visualization and the plot_state_qsphere function for Q-Sphere visualization. These functions provide an interactive and intuitive way to understand the state of your qubits.
References
[1]https://spectrum.ieee.org/transistor-history
[2] Nielsen, Michael A., and Isaac L. Chuang. 2012. “Quantum Computation and Quantum Information.” Cambridge University Press. https://doi.org/10.1017/cbo9780511976667.
[3]https://arxiv.org/pdf/2112.08863.pdf
[5]https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.106.130506
[6]https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.2.020343
[8]https://www.nature.com/articles/s41586-023-06927-3
[9] Couteau, C., Barz, S., Durt, T. et al. Applications of single photons to quantum communication and computing. Nat Rev Phys 5, 326–338 (2023). https://doi.org/10.1038/s42254-023-00583-2
[10] https://arxiv.org/abs/1904.06560